Morphogenesis of Spatial Configurations

Building on the work on Evolutionary Computation, this research investigates generative rule systems for the conceptual design of spatial configurations. The aim is to develop a “creative” evolutionary system. Creativity in this context refers to the ability of such a system to generate solutions whose performance improves over successive generations as their body plan (the structural topology) evolves. Another important aspect that enables creativity is interaction with the user (the designer), who collaborates with the system to steer evolution, supported by well-defined design criteria evaluated computationally (e.g., structural stability).

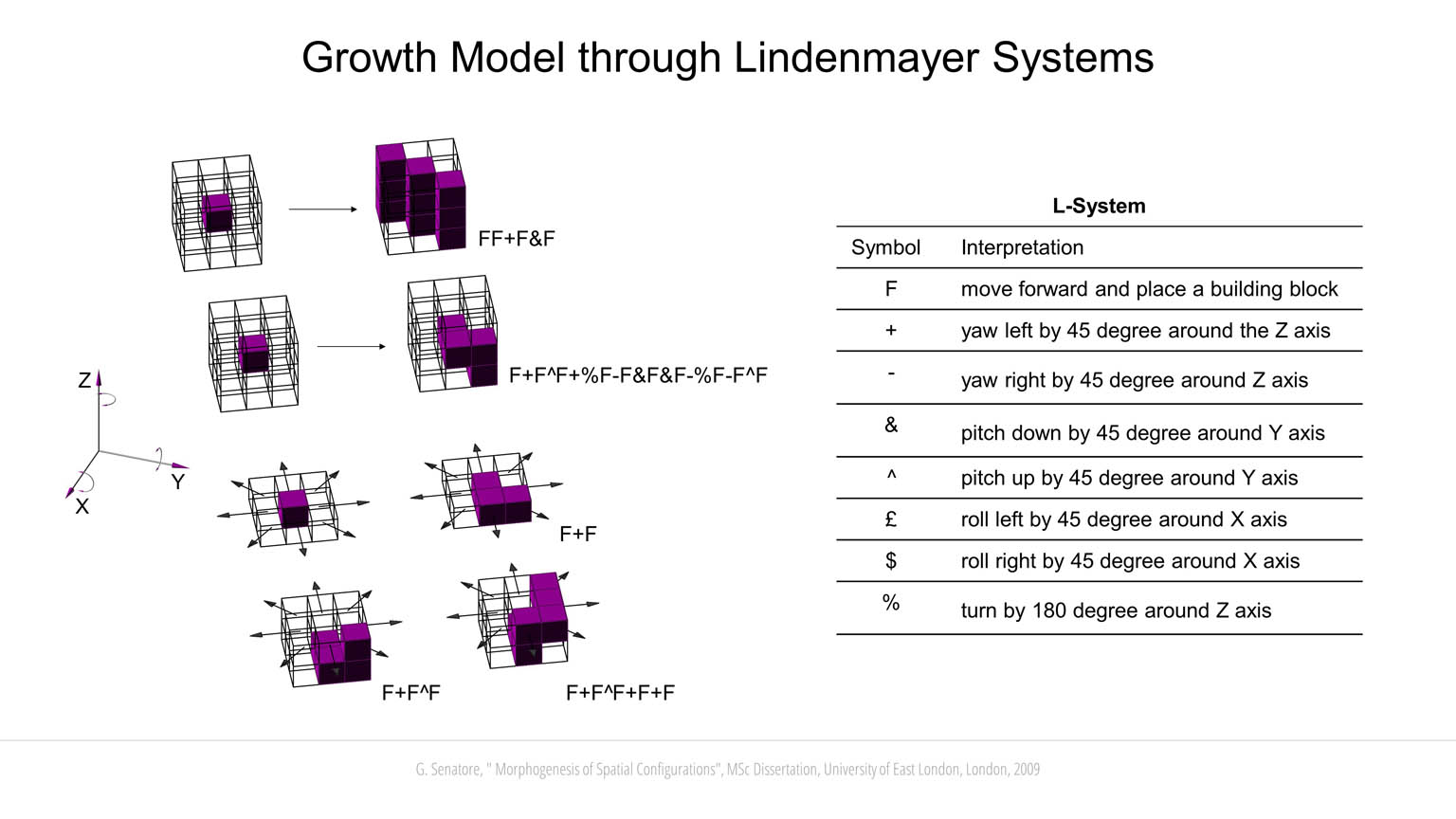
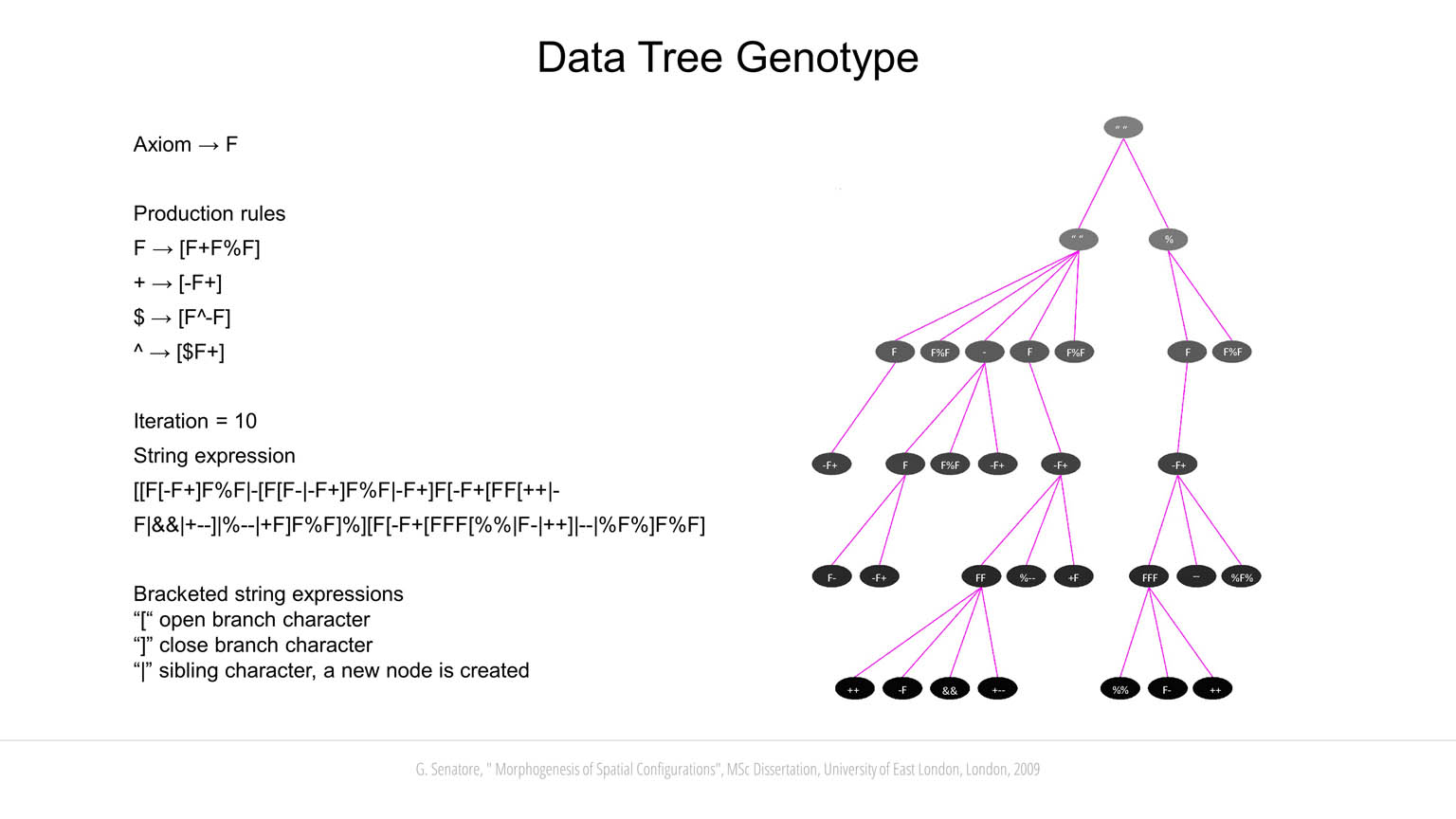
The design methodology developed through this research combines Genetic Programming (GP) and Lindenmayer Systems (L-Systems). GP can be considered a generalization of Genetic Algorithms (GA). The main difference is that, in GP, the genotype has a component-based structure in the form of a data tree, replacing the sequential string of binary numbers used in GA. The data tree contains the rules that define the developmental process. This means that the body plan is not predetermined; instead, it results from evolution. A data tree can be visualized as comprising a root, branches, and leaves. A joint between two branches can be thought of as a node that contains information. A node can be either an “operand” or an “operator.” An operand is an argument for the function performed by the operator. At the ends of the tree, there can be only operands (also called terminals). Nodes on lower-level branches can be both operands and operators. By following the tree hierarchy, one can traverse the tree from its leaves to its root to express the phenotype encoded within it. Each node can contain different data types, recursive procedures, subroutines, or other processes.

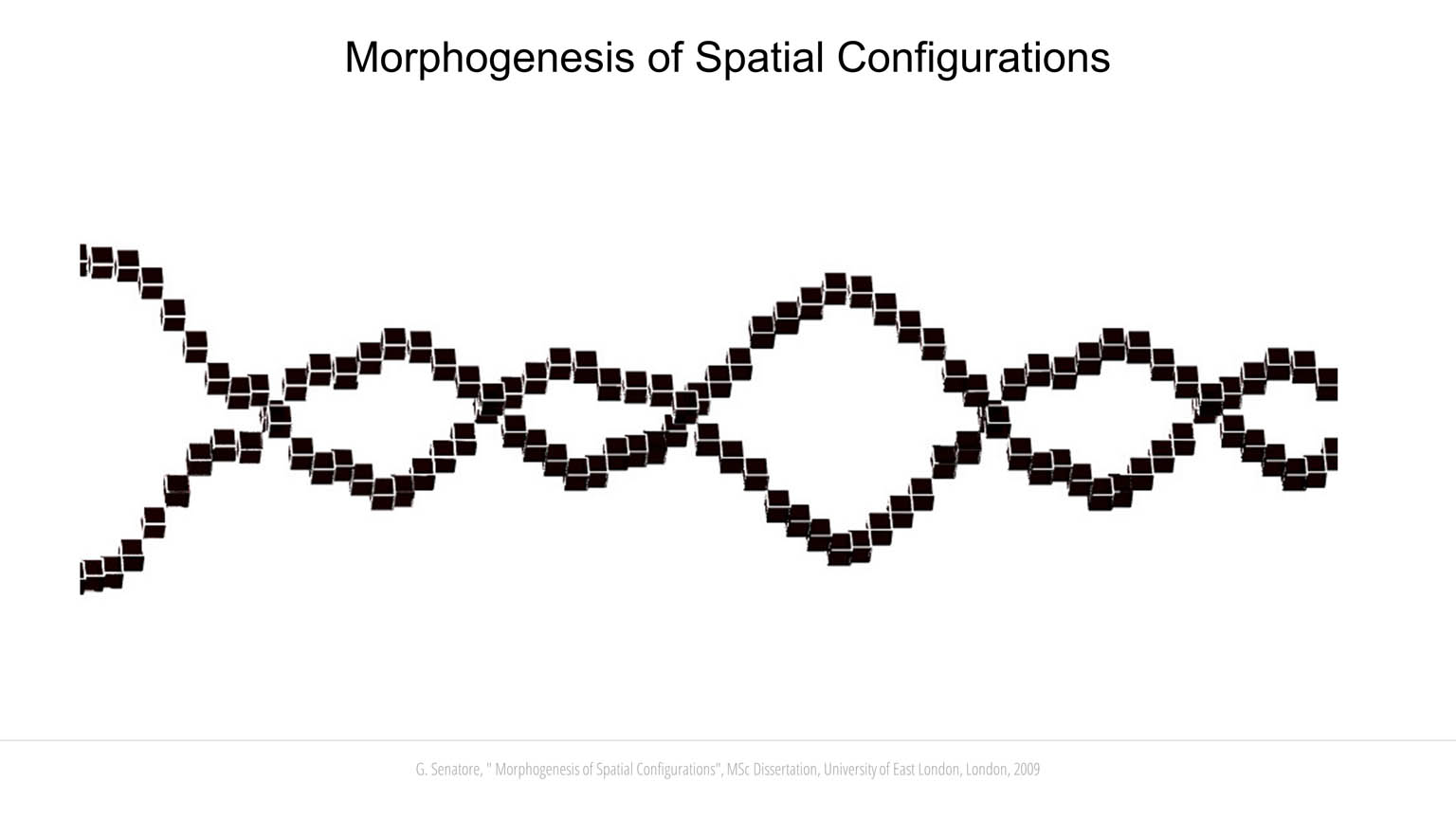
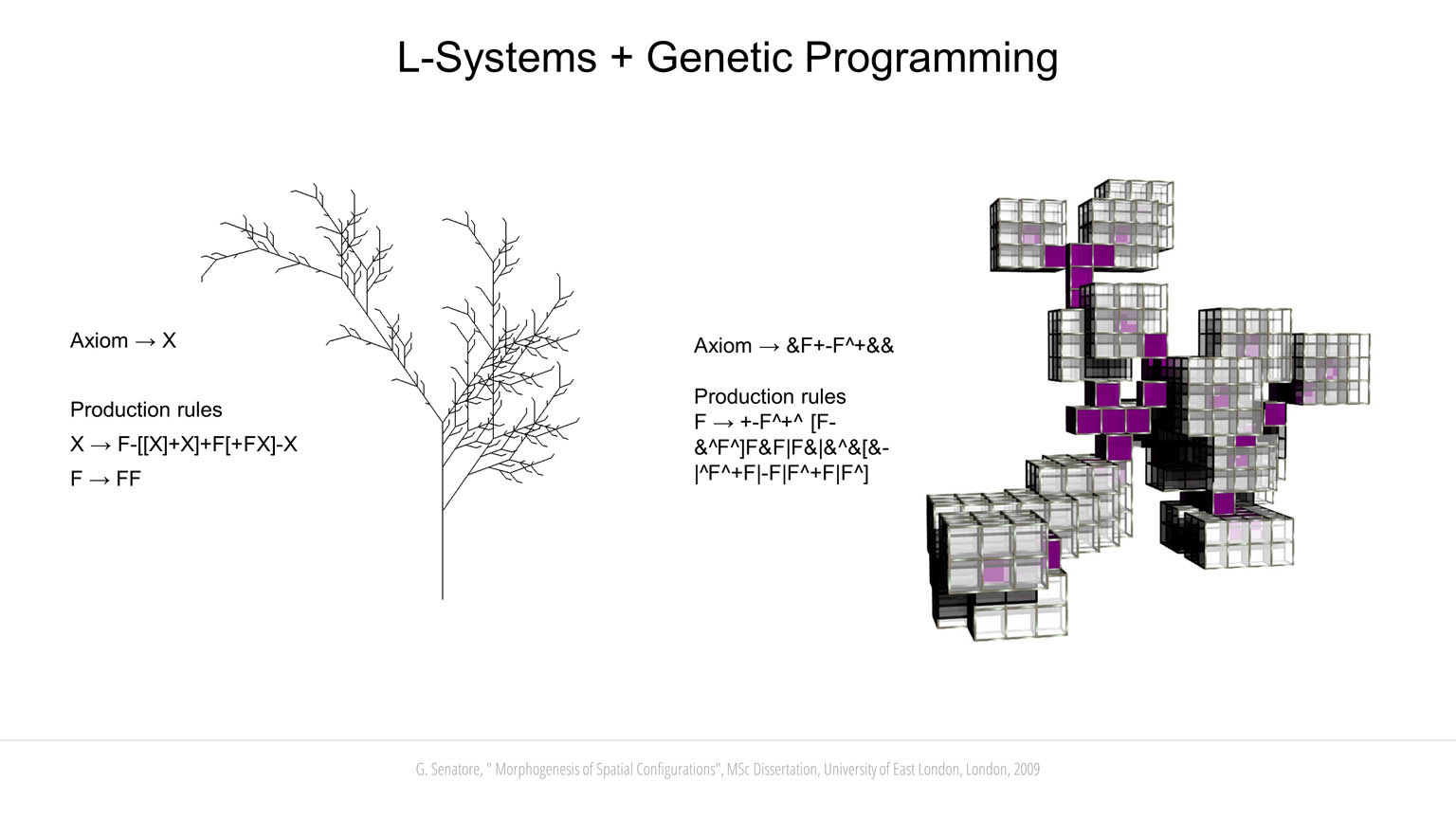
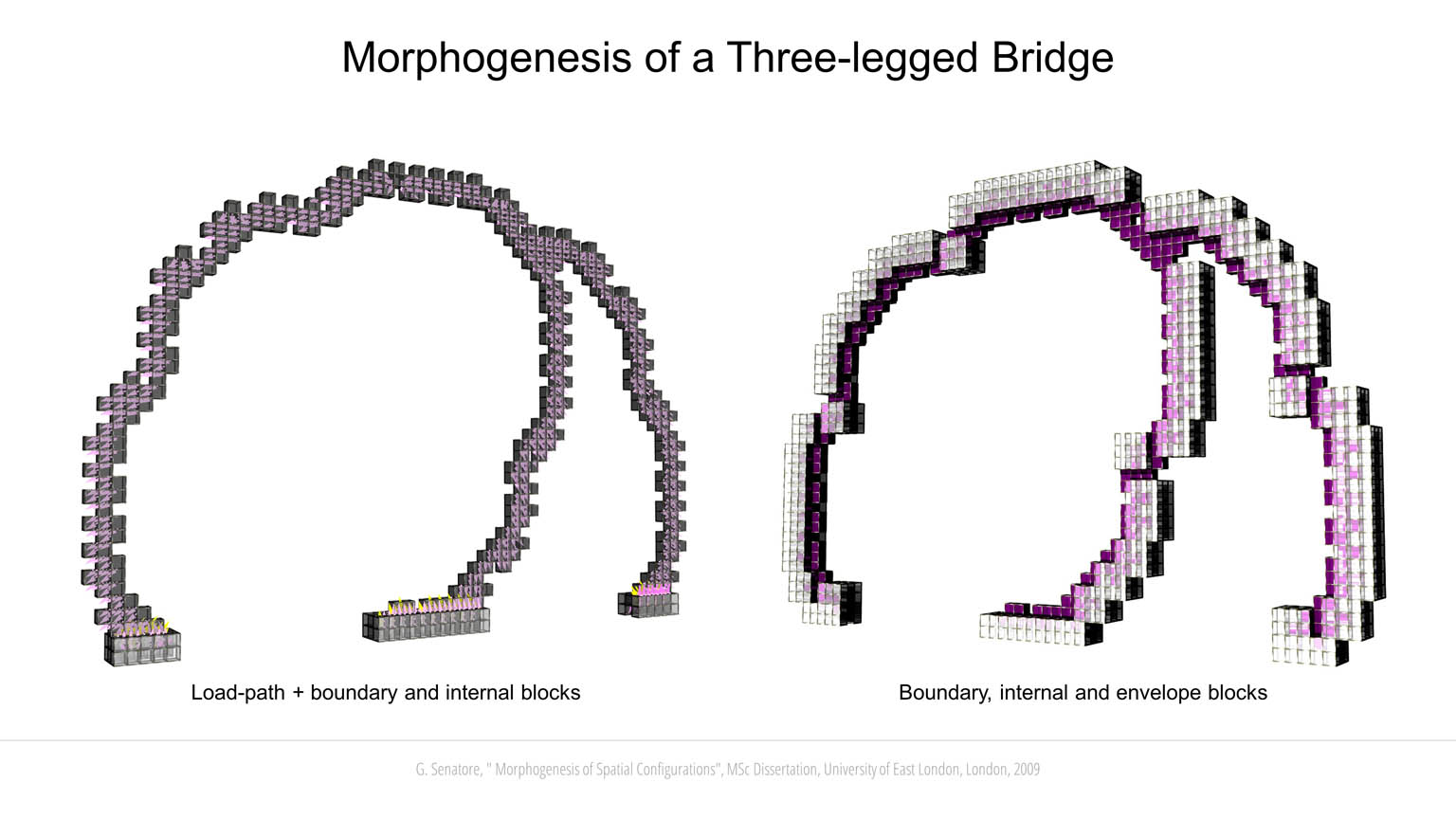
L-Systems are employed to simulate a morphogenesis process. They are based on rewriting rules whereby characters in a string are replaced by other symbols. The string that initiates the rewriting procedure is called the axiom, while the rules that specify which characters in the axiom are replaced by other symbols are called production rules. The symbols are interpreted graphically in a 3D environment. For example, in this work, the character “F” means “move forward” and place a building block (a cube); “+” and “-“ mean yaw left and right, respectively, by 45 degrees around the Z-axis; and “pound” and “$” mean roll left and right, respectively, by 45 degrees around the X-axis. A new block can be generated only from existing blocks, except for the first seed block. Following the biological analogy, a building block can be thought of as a cell in an organism, while the process by which the blocks are assembled represents the growth of the individual. To form the genotype of a candidate solution, an axiom and production rules are first generated randomly, and a string of symbols is created through rewriting. Bracketed expressions are used to parse the string into a data tree. When an open branch character “[” is encountered, a new branch is created. When a closing branch character “]” is encountered, the header returns to the node position containing the corresponding open branch character.

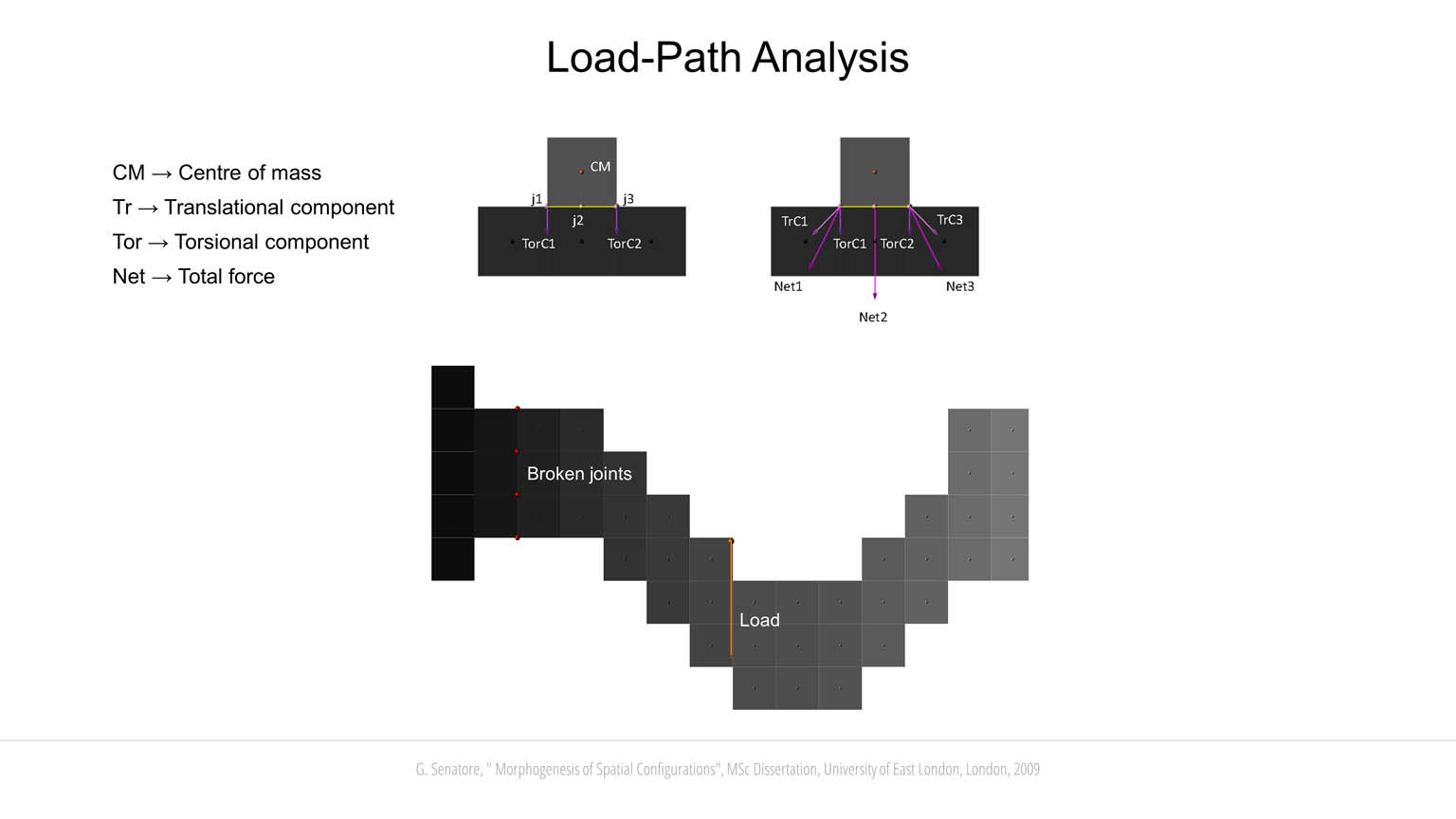
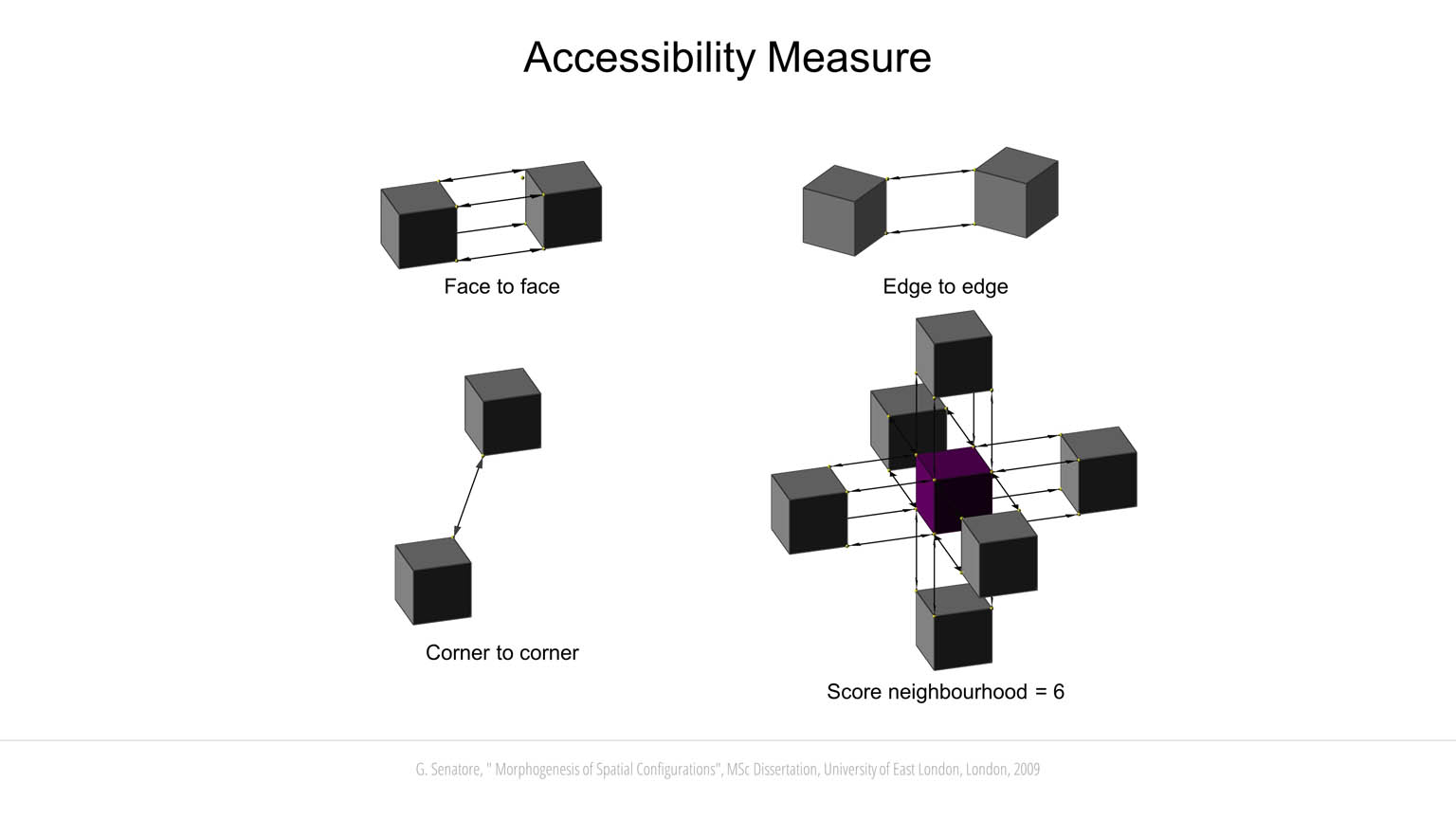
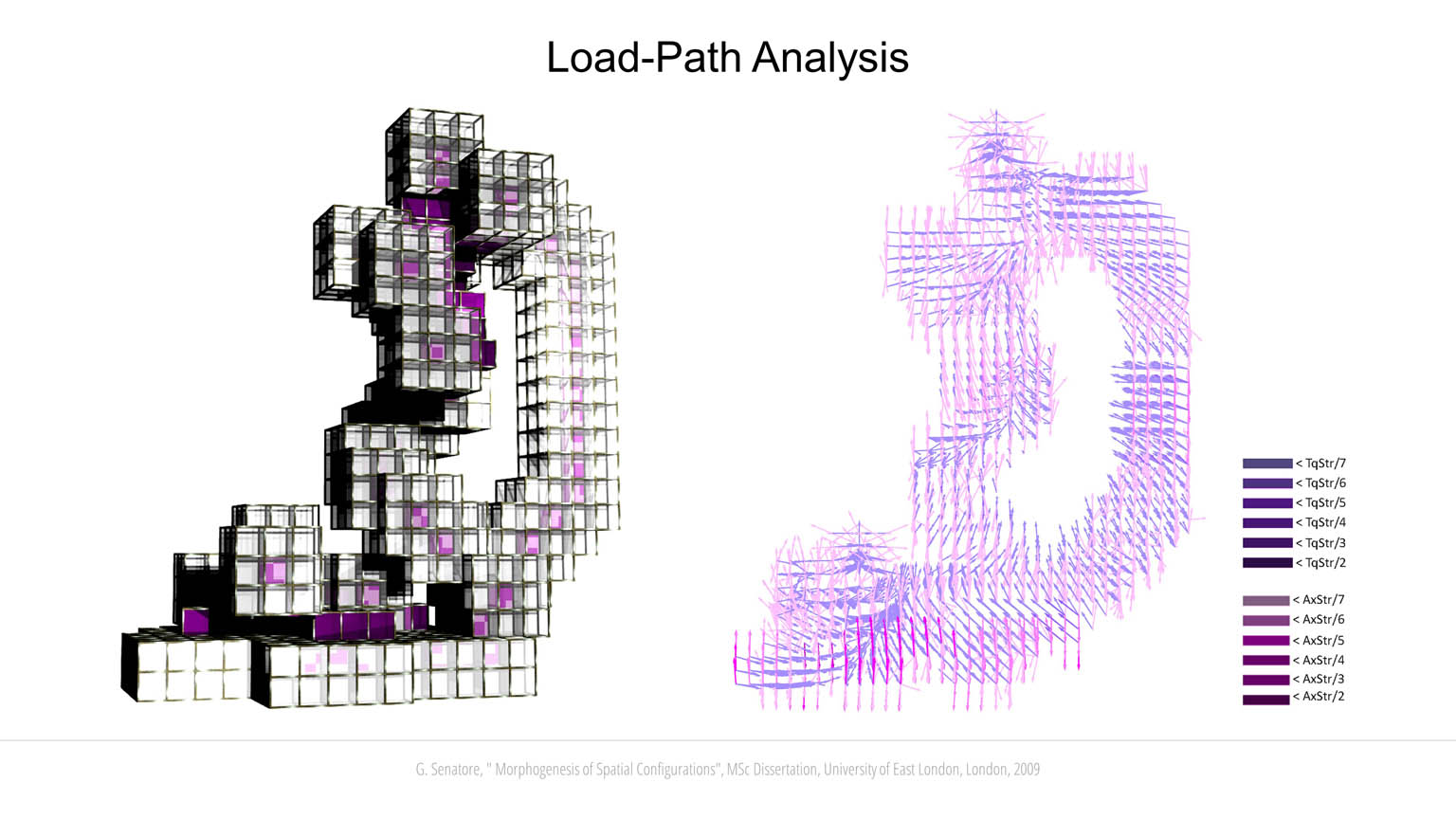
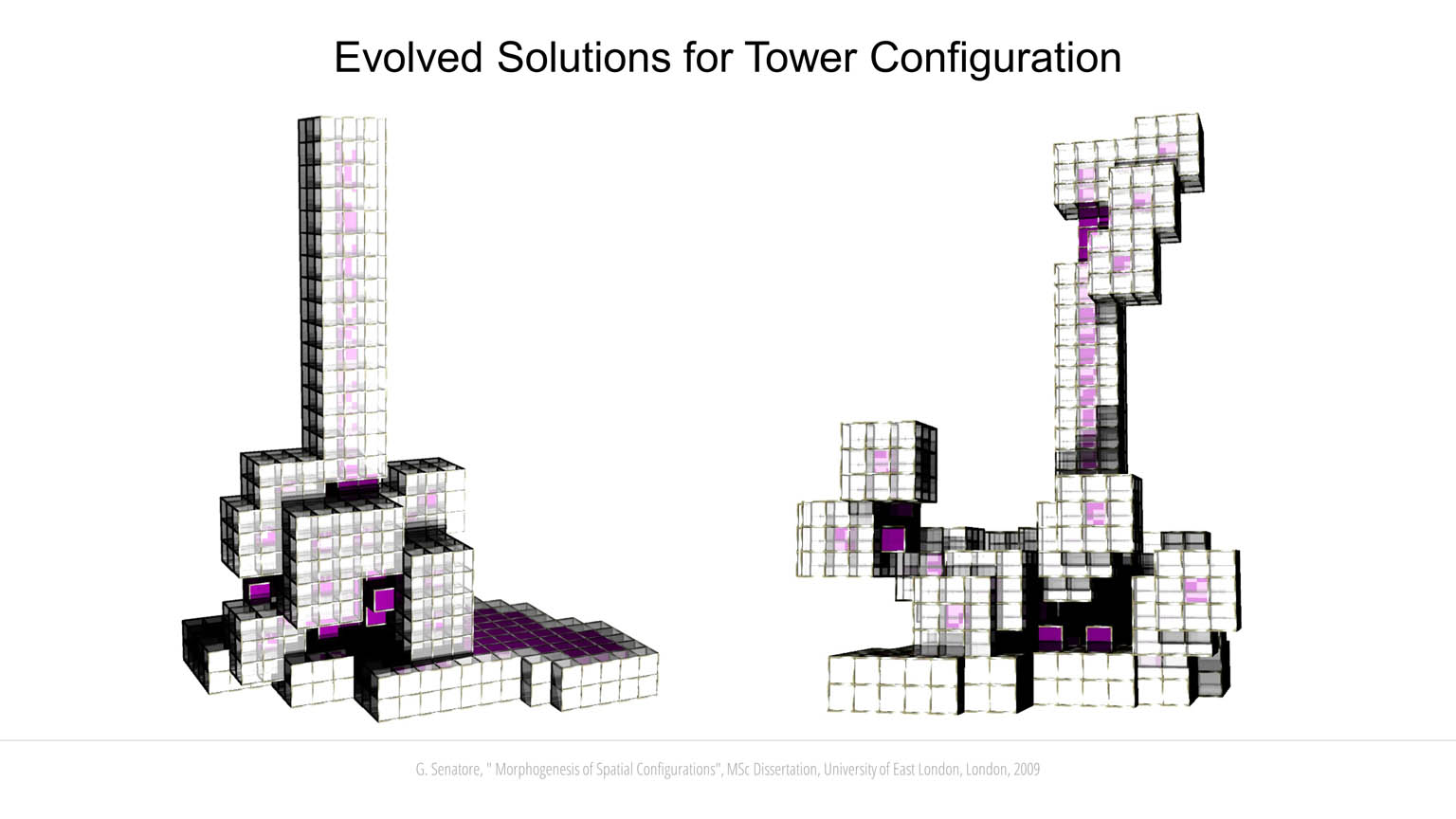
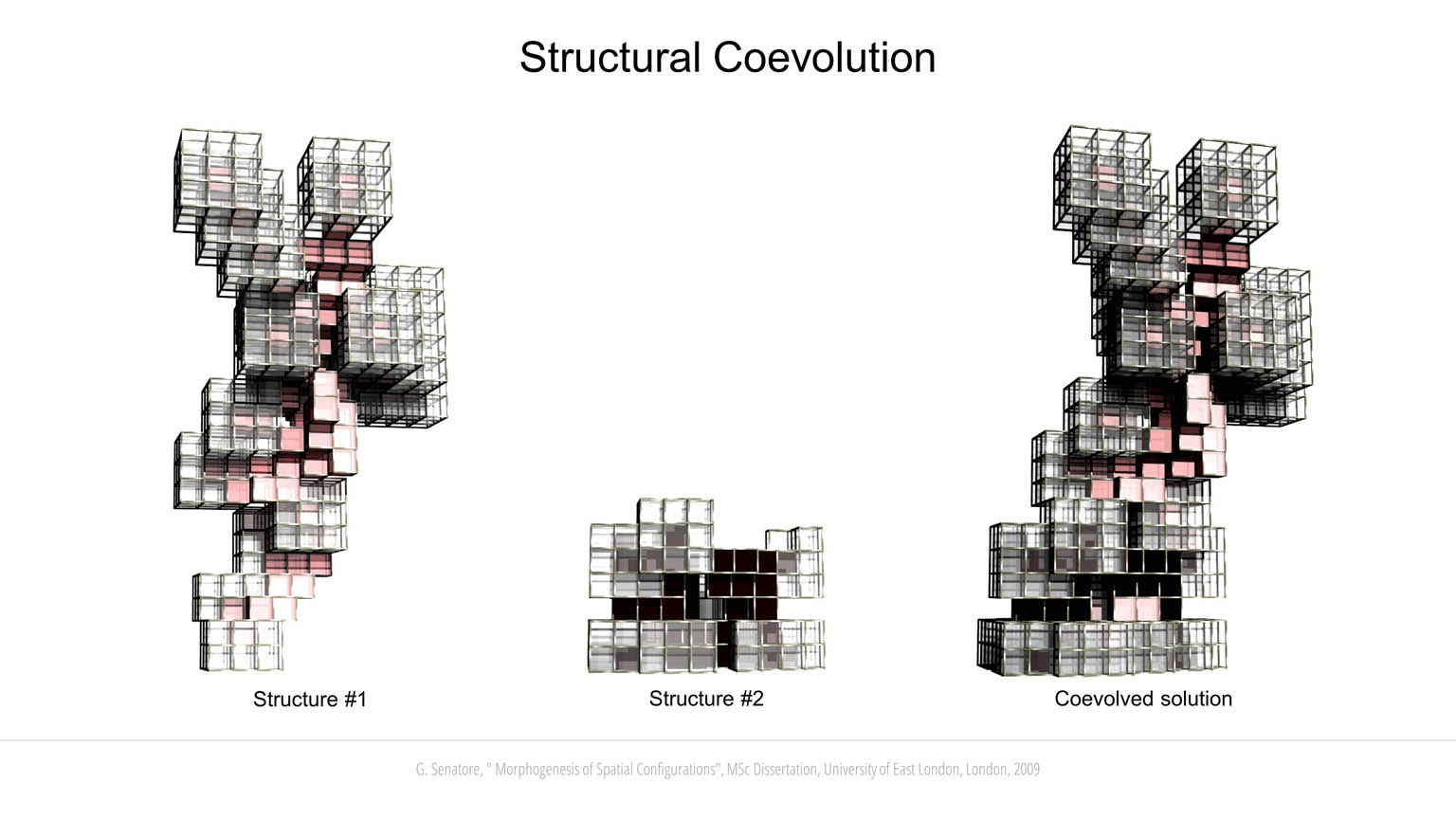
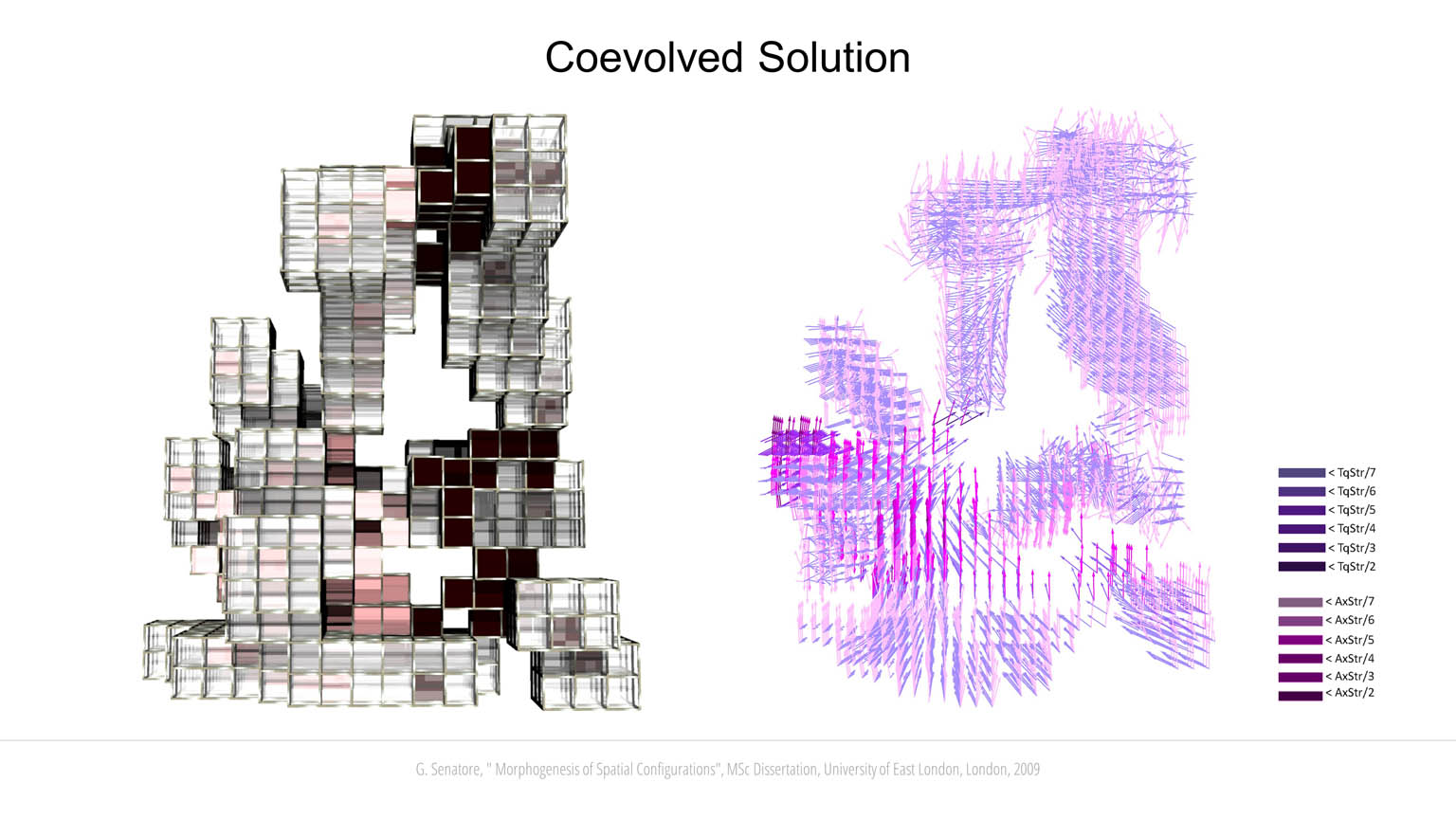
Candidate solutions are evaluated against different design criteria. A simplified structural analysis has been implemented to evaluate the stability of each configuration as it grows. The building blocks are connected through joints located along the edges and at the vertices. Blocks and joints are assigned predefined mechanical properties, including tensile, shear, and flexural strength. Gravity load is applied as a vector field acting on each block. Since new blocks can be generated only from existing blocks, it is possible to simulate a development process similar to the growth of trees and bones. When a new layer of building blocks is formed, the temporary substructure is analyzed. If a failure occurs at any stage of the development process, the genotype of the configuration under development is not passed on to subsequent generations. A multi-objective fitness function couples structural stability with other objectives that depend on the type of configuration being evolved. For example, bridge-like configurations emerge when the objective function rewards solutions that develop a long span orthogonal to the Z-axis. Likewise, tall configurations emerge when the fitness score is proportional to the height of the candidate solution. Another important criterion is a measure of “accessibility,” computed by evaluating the topology of the neighborhood of each building block. Face-to-face connections are assigned the highest score, followed by edge-to-edge and vertex-to-vertex connections. A block that shares a face with one of its neighbors is assigned a higher score because it is more accessible from that neighbor than from one sharing an edge or vertex. The fitness score determined through this analysis measures the connectedness of the spatial configuration as a whole. Co-evolution has been investigated by allowing two initially separate individuals to interact and cooperate to improve performance under the defined design criteria. If the co-evolved solutions share common spaces during development, their genotypes are merged to create a single individual. In some cases, two separate unstable structures have merged to support each other and achieve structural stability.

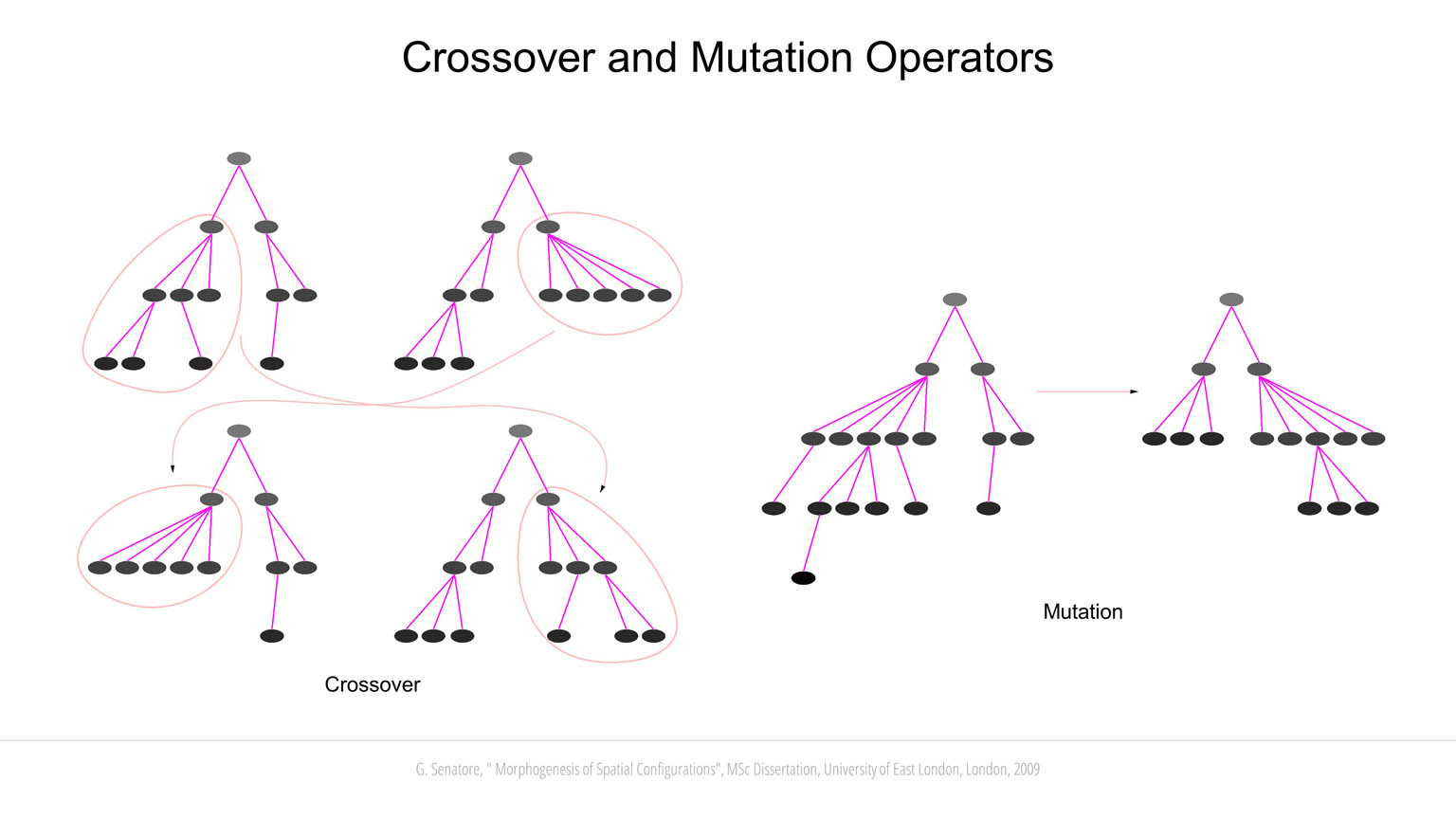
Starting from the randomly generated initial generation, new individuals are created through crossover and mutation. When crossover is performed, a data-tree node from one solution is swapped with a node from another solution, thereby replacing an entire branch. Mutation is implemented by deleting or adding branches and by changing the operand or operator of a single node. When using Genetic Programming, solutions in successive generations can differ significantly due to the effects of genetic operators (crossover and mutation). This can lead to the loss of good solutions. For this reason, a selection operator based on elitism has been adopted. In contrast to fitness-proportionate selection, elitism passes a certain number of the best-performing solutions to subsequent generations. These solutions remain unaltered until better-performing individuals are obtained. Selection also occurs through human interaction. The user periodically evaluates a set of best-performing solutions and selects a subset for subsequent generations.

The combination of L-Systems and Genetic Programming, along with user interaction, has produced a system that generates solutions of increasing complexity over successive generations. In contrast to previous work on Evolutionary Computation, the solution domain comprises not only variables (operands) but also a set of functions (operators) that operate on those variables. The outcome of this research has met the intended aim of developing a creative evolutionary system. Although the search space is inherently discontinuous because the solution body plan evolves, there is positive feedback between the solutions produced by the evolutionary system and their selection through evaluation of the design criteria and user interaction. Working with the evolutionary system has occasionally been surprising, as it has produced nonintuitive yet high-performing solutions.